Lecture notes for Stat665
Cross-entropy cost function
Learning slow is due to the shape of the sigmoid function.
When we use sigmoid function, then the partial derivative of the quadratic cost function for the weight and bias are multiplied by \(\sigma'(z)\). For example, when the desired output is near 0 while the actual output is 1, then the learning is slow although the neuron’s performance is bad.
[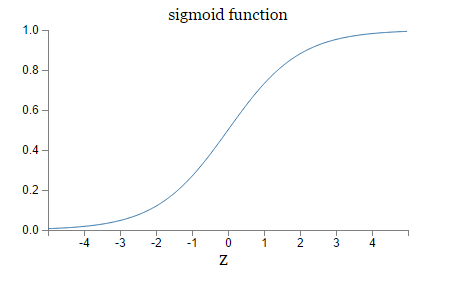 ]
As we can see, the curve tends to be flat when Z is bigger.
]
As we can see, the curve tends to be flat when Z is bigger.
Thus, we need a better function than the trivial quadratic cost function. And cross-entropy is one of the alternatives. The cost function is \(C = -\frac{1}{n} \sum_x \left[y \ln a + (1-y ) \ln (1-a) \right],\) With some algebra calculation, we can prove that the partial derivative of the cost function for weights and bias is independent of \(\sigma'(z)\). And it is only related with \(\frac{\partial C}{\partial w_j} = \frac{1}{n} \sum_x x_j(\sigma(z)-y),\)
And it is worth noting that
the cross-entropy is nearly always the better choice, provided the output neurons are sigmoid neurons.
Basis function
By inserting knots, we got more piecewise cubic polynomials to fit, which enables us to fit more complex functions.
However, without constraint on the border, we may undergo discontinuity on the boundary. To fix this problem, we can (1) force the polynomial to be continuous at the knot by modifying our model (2) we can add indicator functions or truncating function $(x_i-c)_+$ to make a uniform equation.
By this will only make the knot point continuous but not no continuous derivative. So we add the continuity condition on the first&second derivative of the function.
We can also add additional constraint to two ends of the curve.
We should also pay attention to the position of knots and how many knots should we put. Cross-validation can be used to choose the number of knots.
Week10
- Nearest neighbor doesn’t suffer from over-fitting as regression that much.
- Gini index can be used to measure the importance of variable in tree-based classifiers.
- gbm package for boosting
- Default variable numbers tried in “randomforest” package tried:
if (!is.null(y) && !is.factor(y)) max(floor(ncol(x)/3), 1) else floor(sqrt(ncol(x))) - Bootstrapping generates multiple trees and bagging summarizes them together.
- Randomforest uses different subsets of variables at each iteration.
- Boosting tree added variables sequentially.
- One easily-made mistake for randomForest package is that, when the levels of train and test data are not the same, like if you have a variable with level==[0,1] but it all equals 0 in the test set, then there will be a problem when you predict the test set using the trained model. So you have to preset all the predictor levels in the test set equal to the ones in training set.